Método Promethee II para priorização de projetos
flexM4I > abordagens e práticas > Método Promethee II para priorização de projetos (versão 1.3)
Autoria: Prof. Dr. Lucas Gabriel Zanon ([email protected]) - Agradecimentos
Conteúdo desta página
- 1 Descrição resumida
- 2 Quando você deveria utilizar a priorização de projetos baseada no Promethee II?
- 3 Por que você deveria utilizar priorização de projetos baseado no Promethee II?
- 4 O problema da média ponderada na priorização de projetos e o que é compensação e não compensação
- 5 Características dos métodos não compensatórios
- 6 Promethee II
- 7 Conceitos e lógica do PROMETHEE II
- 7.1 Estabelecimento dos critérios de avaliação dos projetos
- 7.2 Definição dos pesos dos critérios
- 7.3 Construção da matriz de pontuação dos projetos
- 7.4 Matrizes de sobreclassificação
- 7.5 Matriz de grau de sobreclassificação
- 7.6 Fluxos no PROMETHEE
- 7.7 Priorização das alternativas
- 7.8 Regras de sobreclassificação
- 8 Atividades para aplicação do Promethee II
- 9 Exemplos de critérios
- 10 Premissas, dicas e cuidados
- 11 Material de apoio
- 12 Promethee II: exemplo de aplicação
- 13 Informações adicionais
- 14 Análise e métodos semelhantes
- 15 Agradecimentos
- 16 Referências
Descrição resumida
O método PROMETHEE II (Preference Ranking Organization Method for Enrichment Evaluation) é um método não-compensatório de priorização de alternativas considerando múltiplos critérios, como por exemplo, na priorização de projetos de inovação.
| A característica não-compensatória deste método é uma vantagem sobre os métodos de priorização e seleção de alternativas (como projetos ou ações) que usam a média ponderada, como explicamos no tópico “O problema da média ponderada na priorização de projetos e o que é compensação e não compensação”. |
A aplicação deste método inicia-se com a definição de critérios independentes, não-redundantes, porém coerentes, com relevância semântica para todas as alternativas (projetos).
| Veja quais são os significados dessas características dos critérios a serem utilizados neste método. |
Esses critérios recebem um peso para influenciar mais ou menos a priorização dos projetos (quanto maior o peso, maior a influência do desempenho de um projeto nesse critério para a sua priorização).
Em seguida o usuário pontua cada projeto com relação aos critérios estabelecidos tomando o cuidado se o maior desempenho de um projeto é diretamente ou indiretamente proporcional ao atendimento do critério.
A partir deste momento, o método PROMETHEE II calcula automaticamente algumas matrizes, que resultam na priorização dos projetos.
| Mais adiante apresentamos essas matrizes, ao explicar quais são os conceitos e a lógica do PROMETHEE II. |
Quando você deveria utilizar a priorização de projetos baseada no Promethee II?
Contexto de Aplicação:
- Projetos com múltiplos critérios de avaliação.
- Situações em que a não-compensação entre critérios é crucial para a tomada de decisão.
- Necessidade de considerar a preferência individual dos tomadores de decisão.
- Projetos onde a personalização dos critérios de avaliação é fundamental.
Quando se quiser evitar a compensação entre os critérios, que é um problema que ocorre no método de priorização de projetos baseado na média ponderada simples
Por que você deveria utilizar priorização de projetos baseado no Promethee II?
- Promove uma abordagem transparente e objetiva na avaliação e seleção de projetos.
- Permite que os tomadores de decisão compreendam claramente como os critérios são aplicados e ponderados na priorização dos projetos.
- Mantém a independência de cada critério, garantindo uma avaliação justa e precisa de cada projeto.
- Evita distorções que podem surgir quando há compensação entre critérios, assegurando que cada critério seja avaliado de forma individual e relevante.
- Permite a consideração das preferências individuais dos tomadores de decisão.
- Oferece flexibilidade para acomodar diferentes perspectivas e prioridades dos stakeholders envolvidos no processo de decisão.
Quais os objetivos que eu posso atingir ao utilizar priorização de projetos baseado no Promethee II?
- Ajuda a selecionar os projetos que melhor atendem aos objetivos da organização.
- Garante que os recursos sejam alocados de forma eficiente e direcionados para os projetos de maior relevância e impacto.
- Reduz o viés e a subjetividade na tomada de decisão, fornecendo uma estrutura objetiva e baseada em critérios para avaliar e priorizar os projetos.
- Contribui para uma gestão mais eficiente dos projetos, priorizando aqueles que têm o potencial de gerar os melhores resultados e impactos positivos para a organização, de acordo com os critérios estabelecidos pelos tomadores de decisão.
O problema da média ponderada na priorização de projetos e o que é compensação e não compensação
Neste tópico discutimos os princípios dos métodos de priorização de projetos baseada na média ponderada simples e destacamos uma das principais limitações desses métodos, que é a compensação entre os critérios.
Média ponderada
Utilizar a média ponderada é uma abordagem comum para priorização de projetos, em que as alternativas são avaliadas por seu desempenho nos critérios de modo ponderado, para atribuir uma pontuação geral a cada projeto.
A próxima figura ilustra um exemplo de média ponderada para seleção de 4 projetos.
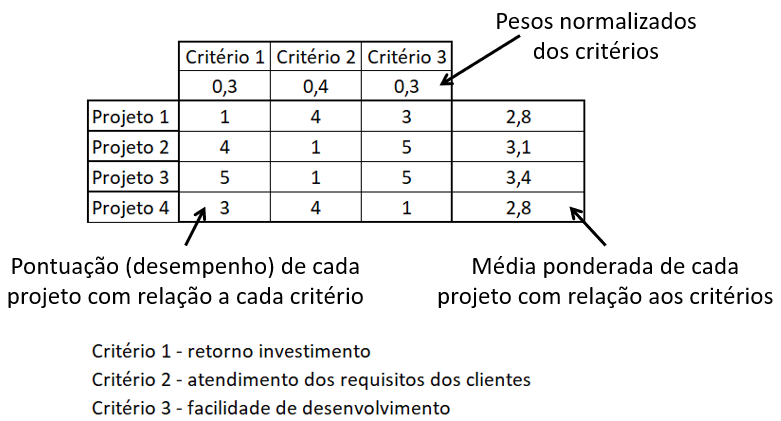
Figura 1176: exemplo do cálculo da média ponderada
Neste exemplo, foram estabelecidos 3 critérios:
- retorno de investimento: quanto maior o retorno de investimento, melhor desempenho do projeto no critério correspondente;
- atendimento dos requisitos dos clientes: quanto maior o atendimento dos requisitos dos clientes, melhor desempenho do projeto no critério correspondente;
- facilidade de desenvolvimento: quanto mais fácil, melhor desempenho do projeto no critério correspondente;
A escala definida para pontuação do desempenho dos projetos nos critérios foi de 1 a 5, sendo 1 a pior pontuação e 5 a melhor. Em outras palavras, um projeto com a pontuação 1 significa que seu desempenho naquele critério é baixo, e, respectivamente, uma pontuação 5 representa o melhor desempenho do projeto no critério avaliado.
| Observe que para simplificar definimos critérios que quanto maior a sua pontuação na escala, melhor desempenho. Se tivesse sido definido o critério “custo”, quanto menor o custo melhor desempenho. Mas para que os projetos possam ser comparados, o valor 1 (menor pontuação e pior desempenho) seria atribuído para o projeto com o maior custo. O valor 5 representaria um projeto com custos baixos (melhor desempenho naquele critério). |
Os critérios têm pesos diferenciados para se realizar a média ponderada. Não importa qual foi a atribuição de pesos para cada critério. Os valores devem ser normalizados, ou seja, a soma dos pesos dos critérios deve ser de 100% (ou 1).
A avaliação de cada projeto resulta da soma das multiplicações da pontuação do projeto em um critério vezes o peso do critério.
Por exemplo, a avaliação do projeto 2 na tabela acima resulta de: 4 x 0,3 + 2 x 0,4 + 5 x 0,3 = 3,5.
No entanto, essa abordagem pode apresentar limitações quando se trata de refletir com precisão as preferências dos tomadores de decisão e as características dos projetos.
Compensação
O método da média ponderada simples é compensatório, ou seja, ele permite que o desempenho excepcional de uma alternativa em um critério seja compensado por um desempenho fraco em outro critério, resultando em distorções na classificação final dos projetos.
Vamos retomar o exemplo do tópico anterior. Para isso, repetimos a tabela com o exemplo das pontuações de desempenho dos projetos nos critérios.

Figura 1176: exemplo do cálculo da média ponderada
Vamos comparar os projetos 1 e 2, cujas avaliações finais foram 2,8 e 3,1 respectivamente. Portanto, o projeto 2 possui uma prioridade maior do que o projeto 1.
O projeto 1 recebeu as seguintes pontuações:
- baixa (1) com relação ao seu desempenho no critério 1 (retorno de investimento);
- boa (4) com relação ao seu desempenho no critério 2 (atendimento dos requisitos dos clientes); e
- média (3) com relação ao seu desempenho no critério 3 (facilidade de desenvolvimento).
O projeto 2 recebeu as seguintes pontuações:
- boa (4) com relação ao seu desempenho no critério 1 (retorno de investimento);
- baixa (1) com relação ao seu desempenho no critério 2 (atendimento dos requisitos dos clientes); e
- elevada (5) com relação ao seu desempenho no critério 3 (facilidade de desenvolvimento).
O desempenho do projeto 2 nos critérios 1 e 3 compensaram o seu baixo desempenho no critério 2.
Os critérios possuem pesos diferentes, e os tomadores de decisão decidiram que o critério 2 (atendimento dos requisitos dos clientes) seria o mais importante para priorizar os projetos. Será que o projeto 2 deve ser priorizado, mesmo tendo um desempenho baixo no critério 2? Ou seja, será que o projeto, que praticamente não atende aos requisitos dos clientes, deve ser priorizado?
Veja só o seguinte exemplo. Imagine um comitê avaliando projetos de pesquisa para financiamento:
- projeto B tem um custo médio, mas risco baixo.
De modo compensatório, o risco alto do projeto A pode ser compensado por seu custo bom. Em outras palavras, o custo bom compensa o risco alto. Esta avaliação pode resultar que o projeto A seja ranqueado nas primeiras posições. O problema é que, por conta disso, estamos incorrendo na possibilidade de selecionar um projeto de risco.
Em uma abordagem de não compensação, o projeto B poderia ser preferido, mesmo com um custo mais alto, porque o risco poderia ser visto como um critério não compensável e vital para o sucesso do projeto.
| Intuitivamente, você pode afirmar que seria só dar um peso mais elevado para o critério risco, que provavelmente, resultaria em uma melhor avaliação do projeto B. Mas como mostramos no exemplo anterior, quando a quantidade de critérios aumenta, assim como a quantidade de alternativas (projetos), as compensações podem ocorrer sem que os tomadores de decisão percebam. |
Outro exemplo, utilizando somente dois critério, seria comparar os seguintes dois projetos:
- projeto G tem um péssimo desempenho no critério “custo” e um bom desempenho no critério “complexidade de desenvolvimento” (é fácil de desenvolver)
- projeto K tem um ótimo desempenho no critério “custo” e um baixo desempenho no critério “complexidade de desenvolvimento” (é difícil de desenvolver)
Nos dois casos, um desempenho em um critério compensa o desempenho no outro critério. Mesmo com ponderação, será que a decisão por um ou por outro é mais acertada?
Os métodos não compensatórios eliminam essas limitações da média ponderada.
Características dos métodos não compensatórios
- A não-compensação entre critérios refere-se a não permitir que o mal desempenho de uma alternativa em um critério seja compensado por seu bom desempenho em outro.
- Mais especificamente, na priorização de projetos, refere-se a não permitir que o mal desempenho do projeto em um dos critérios seja compensado por seu bom desempenho nos outros.
- Na priorização de projetos, a não-compensação entre critérios é importante para garantir que cada critério seja avaliado independentemente, refletindo a verdadeira importância de cada um na decisão final.
O método Promethee II, proposto nesta seção, para priorização de projetos é não compensatório.
Promethee II
O método PROMETHEE foi proposto por Brans, Vincke & Mareschal (1986).
| PROMETHEE – Preference Ranking Organization Method for Enrichment Evaluation. |
Ao contrário de métodos que permitem a compensação entre critérios, o Promethee II mantém a independência de cada critério, garantindo uma avaliação mais precisa e justa.
Isso é particularmente relevante em projetos onde certos critérios não podem ser substituídos ou compensados por outros, como aspectos legais, éticos ou de segurança.
A não-compensação entre critérios no Promethee II oferece transparência e clareza na tomada de decisão, evitando distorções que podem surgir quando há compensação entre critérios.
Família de métodos de apoio à decisão
O PROMETHEE e o PROMETHEE II fazem parte de uma família de métodos de apoio à decisão multicritério desenvolvidos para ajudar na seleção, classificação e ordenação de alternativas com base em diversos critérios, muitas vezes conflitantes. Esses métodos são particularmente úteis para tratar problemas complexos de tomada de decisão em diversas áreas, como gestão ambiental, engenharia, finanças, entre outras.
Esses métodos consideram:
- Critérios com diferentes pesos;
- Dados expressos de forma numérica;
- Avaliação das alternativas separadamente;
- Construção automática de matrizes de comparação par-a-par a partir de regras de sobreclassificação;
- As regras de sobreclassificação garantem a não-compensação de desempenho entre critérios.
| Na lógica do PROMETHEE II explicamos o que são as regras de sobreclassificação. |
Diferenças entre PROMETHEE e o PROMETHEE II
Atualmente o PROMETHEE original é denominado de PROMETHEE I.
PROMETHEE I:
- usado para obter uma pré-ordenação parcial das alternativas;
- útil para identificar grupos de alternativas superiores, mas não fornece uma hierarquia clara e única de todas as alternativas;
- o resultado é uma classificação que pode apresentar indiferenças e incomparabilidades entre as alternativas.
| Indiferença: quando algumas alternativas podem ser consideradas equivalentes. Incomparabilidades: não podem ser diretamente comparadas devido à falta de informações suficientes |
PROMETHEE II:
- estende o PROMETHEE I ao introduzir um ranking completo, superando as limitações de indiferenças e incomparabilidades;
- útil quando for necessário obter um ranking claro e definitivo das alternativas;
- baseado no cálculo de um fluxo líquido para cada alternativa, que considera tanto o fluxo positivo (preferências a favor da alternativa) quanto o fluxo negativo (preferências contra a alternativa);
- as alternativas são então classificadas de acordo com os valores dos seus fluxos líquidos, do maior para o menor.
| Na lógica do PROMETHEE II explicamos o que é fluxo líquido para cada alternativa, como ele é calculado e quais são os fluxos positivo e negativo. |
Conceitos e lógica do PROMETHEE II
Muitas atividades de aplicação deste método são automáticas, realizadas pela planilha Excel que disponibilizamos para você. Se você estiver somente interessado em aplicar, não precisa ler este tópico. No entanto, se desejar entender como este método “funciona”, leia aqui os conceitos e a lógica deste método.
Vamos apresentar os conceitos e a lógica do PROMETHE II com base em um exemplo de priorização de 8 projetos com base em 3 critérios.
Estabelecimento dos critérios de avaliação dos projetos
No nosso exemplo definimos 3 critérios para avaliação dos projetos:
- C1- aderência aos objetivos estratégicos (quanto maior a aderência, maior a preferência pelo projeto)
- C2 – capacidade de desenvolvimento (quanto maior a capacidade de desenvolvimento do projeto com as competências existentes na empresa, maior a preferência pelo projeto)
- C3 – custo (quanto menor o custo do projeto, maior a preferência pelo projeto)
Cuidado ao definir os critérios, pois eles devem ser independentes, não-redundantes, porém coerentes, com relevância semântica para todas as alternativas.
Vamos exemplificar:
Independentes: Cada critério deve ser capaz de avaliar um aspecto específico do projeto sem influência dos outros.
Exemplo: Custo do projeto é independente do tempo estimado de conclusão.
Não-redundantes: Evitar critérios que mensurem o mesmo aspecto, para não considerar mais de uma vez esse aspecto, que resultaria em um peso maior para ele.
Exemplo: Suponha que você está avaliando projetos com base em critérios financeiros. Se você usar tanto “lucratividade anual” quanto “margem de lucro”, você pode estar duplicando a ênfase em critérios financeiros, pois ambos refletem a capacidade do projeto de gerar lucro, apenas de maneiras ligeiramente diferentes. Ao invés disso, escolher apenas um dos critérios evita a redundância e mantém o equilíbrio na avaliação.
Coerentes: Os critérios escolhidos devem ser logicamente consistentes entre si, apoiando o objetivo de avaliação.
Exemplo: Imagine que o objetivo da seleção de projetos é fomentar a inovação tecnológica. Os critérios selecionados, então, deveriam incluir “grau de inovação tecnológica”, “potencial de mercado” e “aplicabilidade técnica”. Estes critérios são coerentes com o objetivo, pois avaliam aspectos fundamentais da inovação em tecnologia de maneira que se complementam, sem desviar o foco do que é essencial para esse objetivo específico.
Relevância semântica para todas as alternativas: Cada critério deve ser aplicável e relevante para todas as opções de projeto avaliadas.
Exemplo: ‘Escalabilidade do projeto’ deve ser um critério válido para todos os tipos de projetos considerados, desde startups a expansões corporativas.
Definição dos pesos dos critérios
Pesos determinam quantitativamente as importâncias dos critérios, numa escala de zero a um. Esses pesos precisam ser normalizados, ou seja, a soma dos pesos deve ser um.
No nosso exemplo, os três critérios definidos receberam os pesos mostrados na próxima tabela.
Tabela 1177: Exemplo de pesos de critérios de avaliação de projetos

Imagine que você considere mais simples dar um peso de 1 a 5 para os critérios. No nosso exemplo, definimos os pesos C1=5; C2: 3; C3=3. A soma desses pesos dá 13. Ao dividir cada um dos pesos por 13 e ao arredondar, você chega aos valores normalizados apresentados na tabela acima
Construção da matriz de pontuação dos projetos
Cada alternativa de projeto irá receber uma pontuação de desempenho, que significa uma avaliação do decisor sobre o desempenho daquele projeto naquele critério.
| Na teoria de apoio à decisão multicritério, essa matriz é denominada de “matriz de decisão”, pois ela é a base da decisão, ou seja, é quando as alternativas são avaliadas de acordo com os critérios. Denominamos aqui de matriz de pontuação dos projetos, pois é o que ocorre, ou seja, cada projeto é pontuado segundo os critérios. A decisão vem depois de processar essas pontuações. |
Matriz 1178: Exemplo de uma matriz de pontuação de projetos (matriz de decisão no PROMETHEE II)
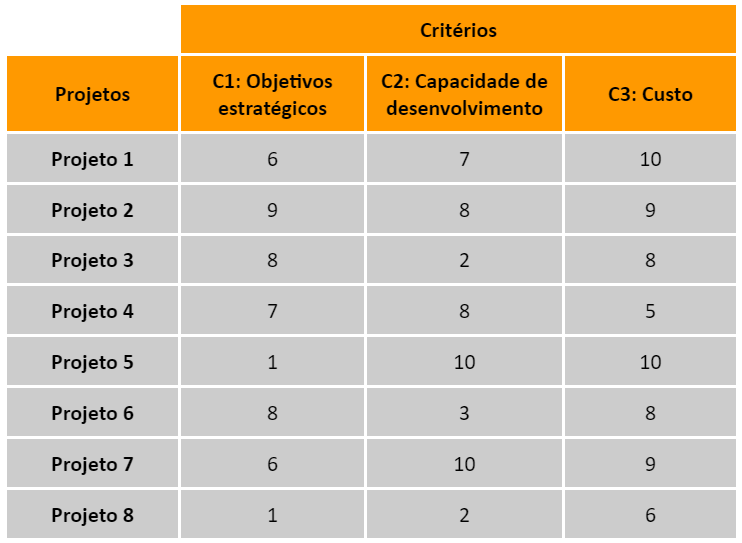
Normalmente, a escala de pontuação vai de 0 a 10. Quanto maior a pontuação, maior o desempenho da alternativa naquele critério.
Na atribuição da pontuação é importante considerar se o critério é diretamente ou inversamente proporcional para indicar o desempenho do projeto com relação a um critério específico.
Por exemplo, se um critério for “alinhamento com os objetivos estratégicos da empresa”, e o decisor avaliar que um projeto está bem alinhado com a estratégia, ele pode determinar um valor 8 para o desempenho do projeto nesse critério. No caso do critério “custo” é o inverso. Se o decisor considerar que um projeto é, relativamente, o de menor custo, ele recebe a pontuação 10.
Nos critérios diretamente proporcionais, quanto mais o critério é atendido, maior a pontuação. Por exemplo, quanto mais um projeto for “alinhado com os objetivos estratégicos da empresa”, maior a pontuação.
Nos critérios indiretamente proporcionais, quanto mais o critério é atendido, menor a pontuação. Por exemplo, quanto maior “o custo de um projeto”, menor a pontuação.
Matrizes de sobreclassificação
A quantidade de matrizes de sobreclassificação é igual a quantidade de critérios. É construída uma matriz de sobreclassificação para cada critério. Cada matriz, relacionada com um critério, compara todos os projetos entre si. Por isso, a quantidade de linhas e colunas é igual a quantidade de projetos.
Sobreclassificação
Sobreclassificação é um processo de comparação do desempenho de uma alternativa de projeto com outra alternativa considerando um único critério.
Considerando que:
- a pontuação (avaliação) de um projeto A com relação a um critério “j” é expressa por gj(a) e
- a pontuação (avaliação) de um projeto B com relação ao mesmo critério “j” é expressa por gj(b) )
Se:
- a pontuação de A for maior que a pontuação de B, ou seja gj(a) > gj(b) , dizemos que o projeto A superou (outranking) o projeto B com relação ao critério “j”, e a comparação (sobreclassificação) recebe o valor “1”.
- a pontuação de A for menor ou igual que a pontuação de B, ou seja gj(a) gj(b) , dizemos que o projeto A não superou (outranking) o projeto B com relação ao critério “j”, e a comparação (sobreclassificação) recebe o valor “0”.
Exemplo de sobreclassificação
Vamos elucidar a sobreclassificação com exemplos.
Por exemplo, suponhamos que um projeto A tenha o desempenho 8 e o projeto B o desempenho 7 com relação ao critério de “alinhamento com os objetivos estratégicos da empresa”. Então, dizemos que A tem um desempenho superior do que B naquele critério. Quando isso ocorrer, na célula da matriz de sobreclassificação do critério “alinhamento com os objetivos estratégicos da empresa”, no cruzamento da linha do projeto A com a coluna do projeto B inserimos o valor 1.
Se o desempenho do projeto A fosse 5 e o desempenho do projeto B fosse 7 (ou igual a 5), o valor a ser inserido na célula da sobreclassificação seria 0.
Mostramos a seguir a matriz de sobreclassificação do critério “Objetivos estratégicos” baseada na matriz 1178 apresentada anteriormente.
| Lembre-se que o critério “Objetivos estratégicos” significa “Alinhamento com os objetivos estratégicos” e que as matrizes de sobreclassificação são calculadas automaticamente. |
Matriz 1179: Matriz de sobreclassificação do critério “C1: Objetivos estratégicos”
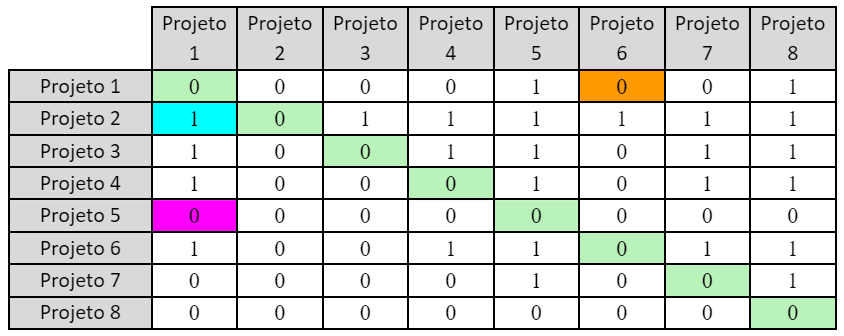
Vamos descrever alguns valores para deixar claro como a sobreclassificação ocorre. Estamos comparando somente os valores da primeira coluna da matriz 1178 de pontuação dos projetos (matriz de decisão), que são relacionados com o critério “Objetivos estratégicos”.
Observe as seguintes comparações:
- O projeto 1 comparado com o próprio projeto 1 tem o mesmo valor, então é inserido automaticamente o valor “0” (assim como todos os outros projetos, marcados em verde claro na matriz anterior).
- O projeto 1 (linha na matriz 1179) recebeu a pontuação 6 no critério C1 (da matriz 1178) e o projeto 6 (coluna na matriz 1179) recebeu 8 no critério C1 (da matriz 1178), então é inserido automaticamente o valor “0”, pois 6 8 (marcado em laranja na matriz anterior).
- O projeto 2 (linha nesta matriz 1179) recebeu a pontuação 9 no critério C1 (da matriz 1178) e o projeto 1 (coluna na matriz 1179) recebeu 6 no critério C1 (da matriz 1178), então é inserido automaticamente o valor “1”, pois 9 > 6 (marcado em azul na matriz anterior).
| O projeto 2 recebeu o valor 9 que é o valor máximo na coluna C1 da matriz 1178. Por isso, na sua linha na matriz 1179 todos os valores são iguais a “1”, a menos da comparação dele com ele mesmo |
- O projeto 5 (linha na matriz 1179) recebeu a pontuação 1 no critério C1 (da matriz 1178) e o projeto 1 (coluna na matriz 1179) recebeu 6 no critério C1 (da matriz 1178), então é inserido automaticamente o valor “0”, pois 1 < 6 (marcado em pink na matriz anterior).
| O projeto 5 e o projeto 8 receberam o valor 1, que é o valor mínimo da coluna C1. Por isso, nas linhas desses projetos na matriz 1179, todos os valores são iguais a zero |
- e assim por diante, é feita essa comparação automaticamente para todas as linhas e colunas da matriz 1179 com base somente da coluna C1 da matriz 1178.
Outras matrizes do exemplo
As outras duas matrizes para os dois outros critérios são apresentadas a seguir.
Matriz 1180: Matriz de sobreclassificação do critério “C2: Capacidade de desenvolvimento”
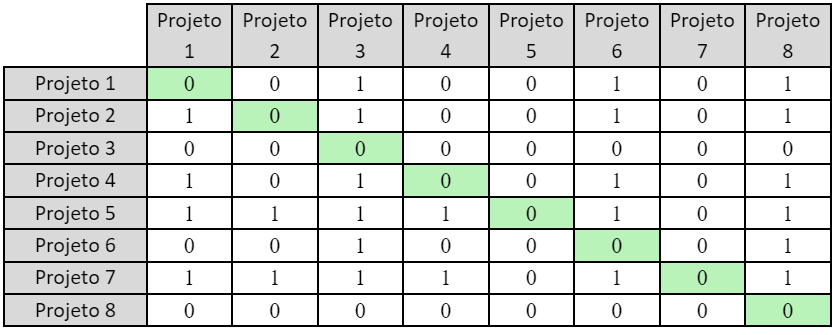
Matriz 1181: Matriz de sobreclassificação do critério “C3: Custo”
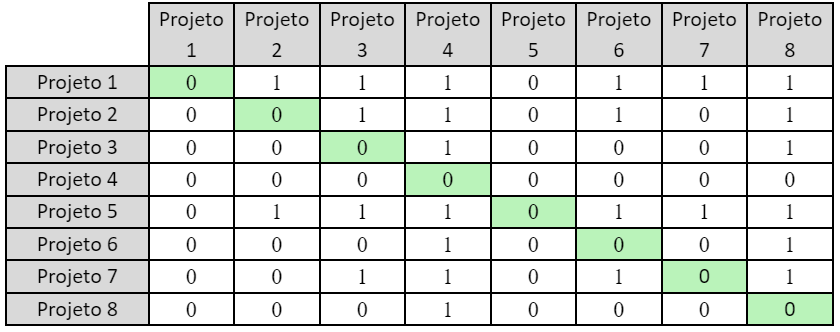

Existem outras regras de sobreclassificação, mas adotaremos a apresentada, que é a mais comum e é conhecida como “preferência estrita”.
As matrizes de sobreclassificação são calculadas automaticamente pelo método PROMETHEE II.
Matriz de grau de sobreclassificação
Essa matriz é a agregação das matrizes anteriores, equivalente a uma soma ponderada dos valores de cada célula das matrizes anteriores, considerando os pesos dos critérios. Ela tem a mesma dimensão que as matrizes anteriores de sobreclassificação.
Essa matriz contém a comparação dos projetos par a par considerando os pesos dos critérios. Ela também é calculada automaticamente com base nas matrizes individuais de sobreclassificação por critérios.
Matriz 1182: matriz de grau de sobreclassificação de 8 projetos com relação a 3 critérios
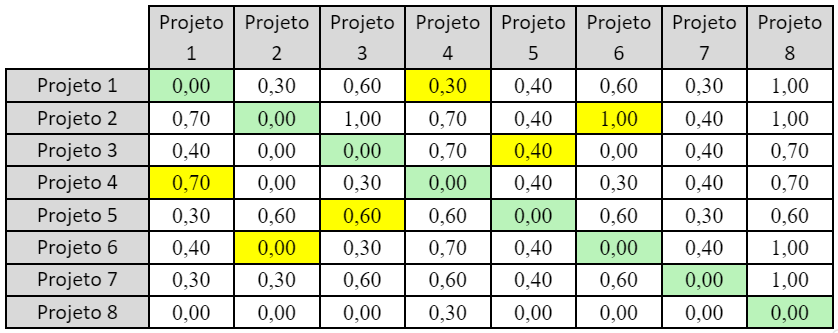
Vamos descrever o cálculo de alguns valores, destacados em amarelo na matriz, para explicar como essa matriz é construída. Os valores destacados em verde na diagonal da matriz mostram que a comparação de um projeto consigo mesmo sempre é nula.
A comparação do projeto 4 com o projeto 1 (célula da linha 4 com a coluna 1):
- Na matriz de sobreclassificação do critério C1, esta célula tem o valor 1, que multiplicado pelo peso do critério C1 (0,4) = 0,4.
- Na matriz de sobreclassificação do critério C2, esta célula tem o valor 1, que multiplicado pelo peso do critério C2 (0,3) = 0,3.
- Na matriz de sobreclassificação do critério C3, esta célula tem o valor 0, que multiplicado pelo peso do critério C2 (0,3) = 0,0.
- A soma desses valores: 0,4 + 0,3 + 0,0 = 0,70.
Observe que a comparação inversa, do projeto 1 comparado com o 4, resulta no valor 0,3, que é o complemento de 0,7 para perfazer 1 (100%).
A comparação do projeto 5 com o projeto 3 (célula da linha 5 com a coluna 3):
- Na matriz de sobreclassificação do critério C1, esta célula tem o valor 0, que multiplicado pelo peso do critério C1 (0,4) = 0,0.
- Na matriz de sobreclassificação do critério C2, esta célula tem o valor 1, que multiplicado pelo peso do critério C2 (0,3) = 0,3.
- Na matriz de sobreclassificação do critério C3, esta célula tem o valor 1, que multiplicado pelo peso do critério C2 (0,3) = 0,4.
- A soma desses valores: 0,0 + 0,3 + 0,3 = 0,60.
Observe que a comparação inversa, do projeto 3 comparado com o 5, resulta no valor 0,4, que é o complemento de 0,6 para perfazer 1 (100%).
A comparação do projeto 2 com o projeto 6 (célula da linha 2 com a coluna 6):
- Na matriz de sobreclassificação do critério C1, esta célula tem o valor 1, que multiplicado pelo peso do critério C1 (0,4) = 0,4.
- Na matriz de sobreclassificação do critério C2, esta célula tem o valor 1, que multiplicado pelo peso do critério C2 (0,3) = 0,3.
- Na matriz de sobreclassificação do critério C3, esta célula tem o valor 1, que multiplicado pelo peso do critério C2 (0,3) = 0,4.
- A soma desses valores: 0,4 + 0,3 + 0,3 = 1,00.
Observe que a comparação inversa, do projeto 6 comparado com o 2, resulta no valor 0,0, que é o complemento de 1,0 para perfazer 1 (100%).

Fluxos no PROMETHEE
O conceito de fluxo
O termo “fluxo” evoca a imagem de algo em movimento, tal como água correndo em um rio. No contexto do PROMETHEE, essa metáfora é usada para representar a forma como as preferências se movem ou são distribuídas entre as alternativas com base nos critérios considerados.
A escolha dessa terminologia visa facilitar a compreensão e a visualização do processo de avaliação e classificação das alternativas. Através dessa metáfora, fica mais intuitivo entender como as alternativas são comparadas entre si dentro do sistema de análise multicritério, permitindo aos decisores visualizar a dinâmica de preferências como fluxos que entram e saem das alternativas, culminando na formação de um ranking.
A denominação “fluxos” no PROMETHEE comunica a essência do método, que é a agregação e comparação das preferências entre as alternativas com base em vários critérios, facilitando o entendimento e a interpretação dos resultados.
Fluxo positivo e fluxo negativo
O fluxo positivo de uma alternativa é uma medida que indica o quanto esta alternativa é preferida em comparação com as outras alternativas, considerando todos os critérios. Um fluxo positivo alto indica que a alternativa é fortemente preferida em relação às outras, segundo os critérios estabelecidos.

Por exemplo, o fluxo positivo do projeto 2, extraído da matriz 1182 do grau de sobreclassificação é a soma de todos os valores da linha 2: 0,7 + 0,0 + 1,0 + 0,7 + 0,4 + 1,0 + 0,4 + 1,0 = 5,2.
![]()
O fluxo negativo de uma alternativa reflete o quanto as outras alternativas são preferidas em comparação com esta, levando em conta todos os critérios. Um fluxo negativo alto sugere que a alternativa é menos preferida quando comparada com as outras, de acordo com os critérios definidos.

Por exemplo, o fluxo negativo do projeto 2, extraído da matriz 1182 do grau de sobreclassificação é a soma de todos os valores da coluna 2: 0,3 + 0,0 + 0,0 + 0,0 + 0,6 + 0,0 + 0,3 + 0,0 = 1,2.
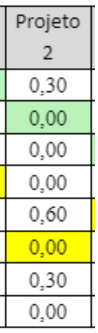
Fluxo líquido como balanço
O conceito de fluxo líquido amplia o conceito do uso da metáfora do termo fluxo, pois representa o balanço entre o quanto de preferência uma alternativa recebe e o quanto ela perde para as outras alternativas.
Assim, o fluxo líquido pode ser visto como um “saldo líquido” de preferências, ou seja, a diferença entre o fluxo positivo e o fluxo negativo de uma alternativa.
| A expressão que representa o fluxo líquido de uma alternativa “a” é: (a) = +(a) ––(a) |
No nosso exemplo do projeto 2, o fluxo líquido é: 5,2 – 1,2 = 4,0.
Um valor positivo do fluxo líquido indica um saldo favorável (mais preferências recebidas do que perdidas) e um valor negativo indica um saldo desfavorável.
| Observe que o cálculo dos fluxos é relativo a uma alternativa (no nosso caso, um projeto). |
Priorização das alternativas
As alternativas (projetos) são priorizadas com base no fluxo líquido. As alternativas com maior saldo líquido obtém uma maior prioridade com relação a outras, como ilustramos no próximo quadro.
Quadro 1183: cálculo dos fluxos positivos, negativos e líquidos de cada projeto com a sua ordenação final (priorização)
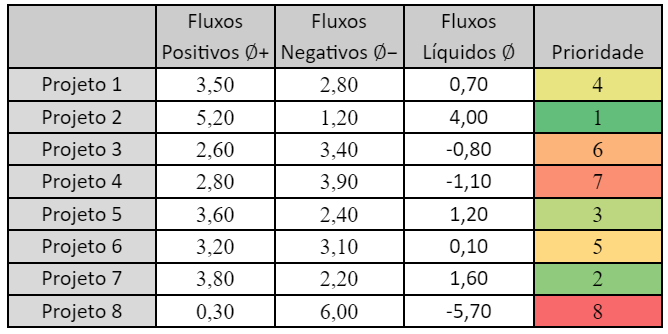
Assim, a priorização desses projetos é:
- Projeto 2
- Projeto 7
- Projeto 5
- Projeto 1
- Projeto 6
- Projeto 3
- Projeto 4
- Projeto 8
Regras de sobreclassificação
Este tópico é voltado para os leitores do nível de detalhamento avançado.
Utilizamos nesta seção a regra de preferência estrita, que é a mais comum de ser aplicada.




Atividades para aplicação do Promethee II
Definir o problema a ser modelado:
- Definir o conjunto de alternativas (projetos) a serem priorizadas.
- A planilha está configurada para avaliar 20 alternativas com base em 6 critérios, utilizando como exemplo a seleção de projetos.
- A quantidade de alternativas e critérios pode ser modificada.
Liste as alternativas (os projetos) a serem avaliadas:
- Preencha no mínimo o nome do projeto na aba “Projetos” para identificá-los.
- Os IDs dos projetos é um código interno da planilha, não os modifique.
- Os demais atributos não entram na lógica da planilha, mas você pode utilizá-los para melhor caracterizar os projetos.
- Os atributos desta aba da planilhas são sugestões, você pode modificar conforme for mais apropriado para a sua organização.
- Esses atributos podem servir para você filtrar os projetos nesta aba.
- A planilha está configurada para 20 alternativas (projetos), se a quantidade for menor ou maior, veja a atividade “Ajuste do número de alternativas (projetos)” descrita mais adiante.
- Como apresentamos no tópico “Premissas, dicas e cuidados” liste projetos que são comparáveis entre si. Ou seja, que possam ser comparados com os mesmos critérios.
Definição dos critérios:
- Defina os critérios que serão utilizados para comparar as alternativas.
- Utilize como referência a aba “Banco de critérios”.
- Copie os critérios selecionados para a aba “Critério”.
- Ou defina seus próprios critérios.
- Copie todas as colunas do critério selecionado (linha) da tabela do banco de dados e cole nas colunas correspondentes na aba “Critérios”. A coluna “Explicação do tipo de critério” é calculada automaticamente.
- Preencha os outros atributos que ajudam a identificar e filtrar
- Considere as diretrizes para se definir os critérios, apresentadas no tópico “Estabelecimento dos critérios de avaliação dos projetos”.
Estabelecimento dos pesos dos critérios:
- Os pesos são inseridos na mesma aba de “Critérios”.
- Para cada critério, o decisor deve estabelecer um peso, que representa o grau de influencia que um critério tem na tomada de decisão, com relação aos outros critérios.
- Os pesos dos critérios são definidos em uma escala normalizada, e a soma dos pesos deve ser 1.
- Existe a alternativa de se dar pesos de 1 a 5 aos critérios , com a normalização automática dos valores para que a soma dê 1.
- Pode haver um decisor único ou um grupo de especialistas (decisores).
- Caso haja um grupo de especialistas, calcula-se a média dos pesos dos critérios estabelecidos pelo grupo (fora da planilha – crie uma planilha simples para essa atividade).
Escalas de pontuação das alternativas (projetos):
- As alternativas (projetos) são avaliadas para cada critério em uma escala de 1 a 10.
- É importante definir se um critério para cálculo do desempenho de projeto em um critério resulta de uma influência diretamente ou indiretamente proporcional.
- Leia sobre isso no final do tópico “Construção da matriz de pontuação dos projetos”.
Pontuação de cada alternativa (projeto) para cada um dos critérios:
- Cada uma das abas amarelas considera um dos critérios.
- As alternativas (projetos) são avaliadas para cada critério em uma escala de 1 a 10.
- Você deve pontuar cada um dos projetos, considerando o critério da aba em questão.
- Repare se a pontuação do projeto segue uma lógica diretamente ou inversamente proporcional.
- Na linha superior da planilha indicamos automaticamente, com base no que você inseriu na aba “Critérios”, quais são os significados dos valores extremos da escala de 1 a 10 para o critério em questão
- Pode haver um decisor único ou um grupo de especialistas (decisores).
- Caso haja um grupo de especialistas, calcula-se a média das avaliações dos especialistas para cada alternativa (projeto) – essa média deve ser calculada fora da planilha, copiando a matriz de cada aba de avaliação do critério para cada decisor.
Cálculos automáticos:
- Todos os cálculos automáticos com base nos pesos dos critérios e pontuação de cada projeto nas avaliações dos critérios (abas amarelas) são registrados nas matrizes da aba “PROMETHEE – cálculos”.
- Você não precisa olhar e nem entender essas matrizes
- Se desejar entender como essas matrizes são montadas, leia o tópico “Matrizes de sobreclassificação” e “Matriz de grau de sobreclassificação”.
Consulta do resultado final:
- O resultado da ordenação final não-compensatória pode ser consultado na aba “RESULTADO”.
- (Obs.: Empates são raros, mas podem ocorrer)
Ajuste do número de alternativas (projetos):
- Para aumentar o número de alternativas, basta adicionar mais linhas na aba “Projetos” e nas abas em amarelo(de avaliação dos critérios para todos os projetos)
- Adicionar também linhas nas matrizes da aba “PROMETHEE – cálculos” e arrastar as fórmulas.
- Para diminuir o número de alternativas, basta apagar linhas nas abas em amarelo e nas matrizes da aba “PROMETHEE – cálculos”.
Ajuste da quantidade de critérios:
- Para diminuir a quantidade de critérios, você deve:
- Eliminar linhas da aba “Critérios”,
- Eliminar a aba amarela correspondente aos critérios eliminados, e
- Apagar as colunas das matrizes da aba “PROMETHEE – cálculos”, que correspondem aos critérios eliminados.
- Para adicionar critérios, você deve:
- Aumentar as linhas da tabela da aba “Critérios,
- Criar uma nova aba para avaliação de cada novo critério,
- Adicionar colunas para os novos critérios em todas as matrizes na aba “PROMETHEE – cálculos”, tomando o cuidado de copiar as fórmulas das colunas anteriores.
Exemplos de critérios
É bastante interessante notar que os critérios devem ser escolhidos de acordo com o contexto a ser modelado. A premissa é que sejam representativos e aplicáveis de maneira homogênea para avaliação de todas as alternativas.
Abaixo, segue um quadro com exemplos de critérios para o caso da seleção de projetos. A tabela completa pode ser consultada na planilha de cálculo, que você pode baixar no tópico “material de apoio”.
Quadro 1184: exemplos de critérios de ponderação de alternativas (projetos)
Fonte: esses critérios foram baseados em um trabalho realizado por Maiara Rosa Cencic e Yukio Shibata
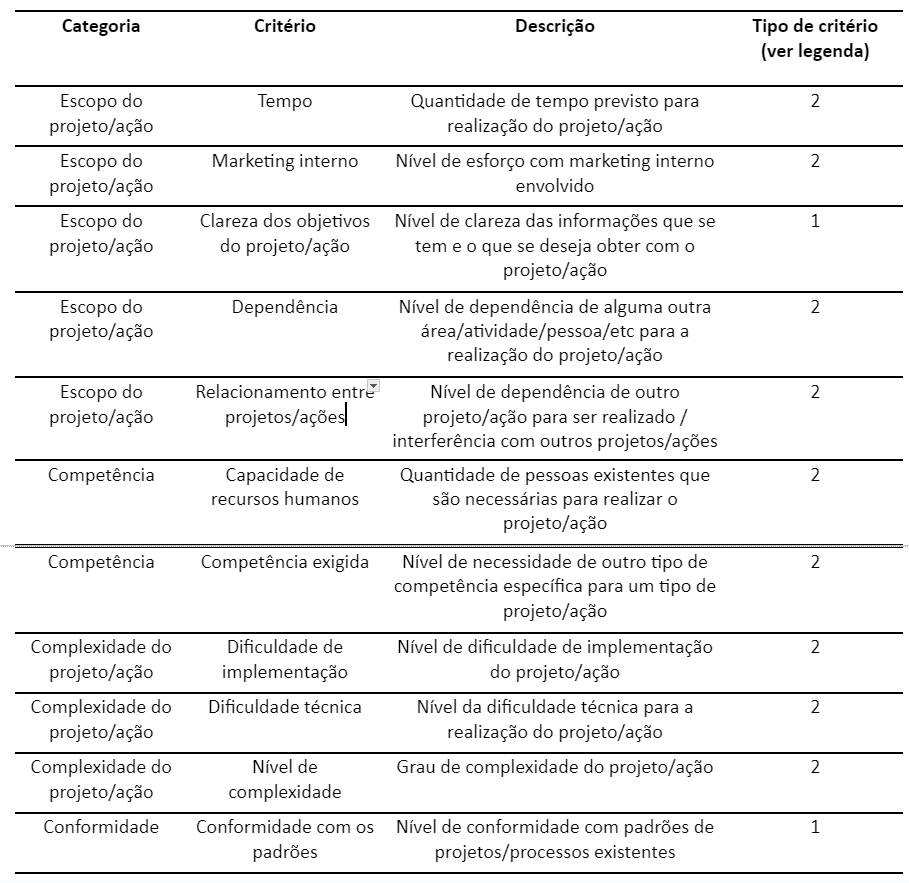
Legenda
1 – diretamente proporcional
2 – inversamente proporcional
Premissas, dicas e cuidados
- Uma premissa fundamental para o sucesso de aplicação desta ferramenta é que as alternativas sejam semelhantes para que todos os critérios de análise possam ser considerados ao se comparar as alternativas. Ou seja, sempre analise alternativas comparáveis.
- Antes de utilizar o Promethee II para a priorização não compensatória de projetos, é crucial estabelecer critérios de avaliação claros e bem definidos, de acordo com o que apresentamos anteriormente, na descrição do tópico “Estabelecimento dos critérios de avaliação dos projetos”.
- Ao aplicar o Promethee II, é essencial manter consistência na avaliação dos critérios entre os diferentes projetos.
- A escolha adequada da escala de medição e a correta ponderação dos critérios são aspectos críticos na aplicação do Promethee II. A sensibilidade a esses fatores pode influenciar significativamente os resultados da priorização.
- É importante considerar a realização de uma análise de sensibilidade por meio da alteração dos pesos e verificação de alterações na ordem final.
Material de apoio
Para fazer download, utilizar, copiar, acessar e/ou se inspirar
- Planilha aberta e adaptável operacionalizando as fórmulas do Promethee II
- No tópico “Promethee II: exemplo de aplicação”, esta mesma planilha está preenchida com um exemplo fictício.
Promethee II: exemplo de aplicação
Informações adicionais
Vídeo-aula prática sobre Promethee II: Sistemas de Apoio à Decisão: Vídeo-aula 4 – Caso de aplicação PROMETHEE II
Esse vídeo aborda, em detalhes, a implementação do método PROMETHEE II no Excel, considerando um caso de aplicação. O intuito é permitir que qualquer um possa desenvolver uma planilha que operacionalize a técnica para apoiar a priorização não-compensatória de alternativas.
Vídeo-aula teórica sobre Promethee: Sistemas de Apoio à Decisão: vídeo-aula 4 – PROMETHEE
Esse vídeo aborda os aspectos técnicos e pormenores matemáticos do PROMETHEE II, destacando como o mecanismo de sobreclassificação garante a não-compensação na técnica.
Análise e métodos semelhantes
No contexto dos métodos PROMETHEE, um aspecto de grande relevância é a facilidade com que os tomadores de decisão compreendem os conceitos e parâmetros subjacentes, simplificando assim a modelagem de preferências e, por conseguinte, aumentando a eficácia da aplicação do método multicritério.
Essa característica representa uma vantagem dos métodos PROMETHEE em comparação com outros métodos de sobreclassificação, como os métodos ELECTRE. A família ELECTRE utiliza os conceitos de concordância e discordância para avaliar as vantagens e desvantagens entre pares de alternativas, o que pode dificultar a implementação do método (Silva, Schramm, Carvalho, 2014). Além disso, os métodos PROMETHEE podem ser facilmente integrados em linguagens de programação computacional, promovendo sua aplicabilidade.
Agradecimentos
Agradecemos o apoio do CNPq no fomento do projeto Processo 408104/2023-6, intitulado “Explorando as relações entre sustentabilidade e percepção de valor pelo cliente: uma abordagem de apoio à decisão multicritério baseada em text analytics”. A presente publicação não é resultado direto do projeto.
Referências
Araujo, A. G.; Almeida, A. T. Apoio à decisão na seleção de investimentos em petróleo e gás: uma aplicação utilizando o método PROMETHEE. Gestão & Produção, v. 16, n. 4, p. 534-543, 2009.
Brans, Vincke e Mareschal (1986) “How to select and rank projects: the PROMETHE method”. European J. O. Research, 24, 228-238.
Silva, V. B. D. S., Schramm, F., & Carvalho, H. R. C. D. (2014). O uso do método PROMETHEE para seleção de candidatos à bolsa-formação do Pronatec. Production, 24, 548-558.
Souza, R. V.; Carpinetti, L. C. R. (2014) A FMEA-based approach to prioritize waste reduction in lean implementation. Int. J. Quality and Reliability Management, 31 (4), pp. 346-366.
