A recursividade ocorre quando a definição de um processo depende de uma versão simplificada do mesmo processo (wikipedia em inglês ).
A Wikipédia em português não apresenta fontes para as explicações, mas no item “recursão em português claro”, ela traz que “A recursão é o processo pelo qual passa um certo procedimento quando um dos passos do procedimento em questão envolve a repetição completa deste mesmo procedimento.”
Em computação, a recursividade é quando uma sub-rotina (função ou método) de um programa computacional pode chamar a si mesmo. Um exemplo clássico é a programação de uma função que calcula o fatorial de um número natural N, ou seja N!.
Por exemplo (adaptado da Wikipédia), o fatorial de 4! é igual a 4 x 3 x 2 x 1 = 24.
Considerando que 0!=1, uma função para calcular o fatorial poderia ser:
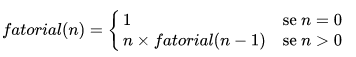
Figura 909 – equação da recursividade
Fonte: Wikipédia (acesso em 31/2/2023)
Aplicando para o exemplo do 4!
fatorial(4) = 4 x fatorial(3) = 4 x3 x fatorial(2) = 4 x 3 x 2 x fatorial(1) = 4 x 3 x 2 x 1 x fatorial(0) = 4 x 3 x 2 x 1 x 1 = 24
Observe que a função fatorial chamou a si própria.
Se não colocarmos um critério de parada, uma função recursiva vai ao infinito, como no caso de um espelho que reflete a si próprio.
